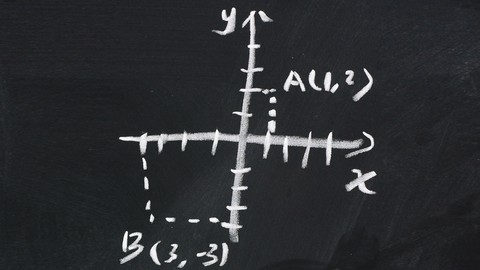Complex numbers are a fascinating and powerful mathematical concept with numerous applications in various fields, including electrical engineering, physics, and signal processing.
By mastering complex numbers, you can gain a deeper understanding of AC circuits, solve complex equations, and unlock a whole new world of mathematical possibilities.
Finding the right complex numbers course on Udemy can be tricky with so many options available.
You want a course that covers the fundamentals, delves into applications, and is taught by an experienced instructor.
For the best complex numbers course overall on Udemy, we recommend "Complex Numbers for Electrical Engineering Students".
This course is designed specifically for electrical engineers and students who want to master the applications of complex numbers in AC circuits.
It starts with the fundamentals of complex numbers and then dives deep into real-world applications, making it an excellent choice for anyone wanting to apply complex numbers to their engineering studies.
While this is our top recommendation, there are other excellent options available on Udemy that focus on different aspects of complex numbers, cater to various learning styles, and cover specific topics like advanced math and IGCSE preparation.
Keep reading to explore our full list of recommendations and discover the perfect complex numbers course for you!
Complex Numbers for Electrical Engineering Students
You will start by building a strong foundation in the fundamentals of complex numbers, including the real and imaginary axes, vectors, and the imaginary unit “j”.
The course dives deep into the two main forms of representing complex numbers - rectangular and polar.
You’ll learn how to convert between these forms with plenty of examples and exercises to reinforce your understanding.
Operations like addition, subtraction, multiplication, and division of complex numbers are covered in detail.
But what really sets this course apart is its focus on practical applications in electrical engineering.
You will explore how complex numbers are used to represent voltages, currents, impedances, and power in AC circuits.
The syllabus covers a range of circuit types, including series, parallel, and mixed RLC circuits with resistors, capacitors, and inductors.
One highlight is the section on phasor analysis, which is crucial for understanding AC circuit behavior.
You’ll also learn how to use complex numbers to derive equations for various AC circuit configurations.
The course even includes a tutorial on analyzing circuits with two sources, demonstrating advanced problem-solving techniques.
Master the Fundamentals of Complex Numbers
The course starts by introducing complex numbers and their basic operations through examples and practices.
You’ll learn to find complex roots of polynomial equations using the Argand diagrams.
Next, you’ll dive into the modulus-argument form, which provides an alternative way to represent complex numbers.
You’ll practice multiplying, dividing, and finding powers of complex numbers in this form.
The course also covers Euler’s formula, which connects complex numbers to trigonometry.
For those aiming for higher levels like IGCSE or college, the course explores advanced topics like loci of complex numbers, including circles, perpendicular bisectors, and half-lines.
You’ll also learn about inequalities involving complex numbers.
If you’re an IB HL or college student, the course takes it further with De Moivre’s theorem and finding nth roots of complex numbers.
Throughout, you’ll find ample practice exercises with detailed solutions to reinforce your understanding.
The course wraps up with problem-solving exercises that test your mastery of complex numbers.
You’ll even get bonus materials like extra videos and written solutions to the quizzes.
Complex Numbers & Polynomials- Both Basic & Advanced
You’ll start with an introduction to complex numbers, their history, and how they relate to real quadratics with delta less than zero.
From there, you’ll dive into the definition of complex numbers, operations on them, and how to solve real polynomials with both real and complex roots.
The course thoroughly explains complex conjugates and their properties, which are crucial for working with complex numbers.
When it comes to polynomials, you’ll learn about their multiplication, division, addition, and subtraction.
The course also covers important concepts like zeros, roots, factors, and polynomial equality.
You’ll study key theorems like the Remainder Theorem, Factor Theorem, and the Sum and Product of Roots.
The course doesn’t just focus on theory; you’ll also learn how to graph various real functions like linear, quadratic, cubic, and quartic functions.
This will help you visualize and better understand complex numbers and polynomials.
One of the highlights is learning about the modulus of a complex number, which allows you to find the distance between two points in the complex plane.
You’ll also explore the argument and polar form of complex numbers, including their properties and solved problems.
The course delves into Euler’s form and De Moivre’s Theorem, which are essential for working with complex numbers.
You’ll learn how to apply De Moivre’s Theorem to find roots of complex numbers, including the cube root of unity.
Throughout the course, you’ll encounter quizzes and worked examples to reinforce your understanding.
You’ll gain a solid foundation in complex numbers and polynomials, making you well-prepared for more advanced topics in mathematics and related fields.
The introduction to Complex Numbers
You will start by learning about the imaginary unit i and its different powers.
Next, you will explore the three main forms of representing complex numbers: Cartesian, polar, and exponential.
The course covers Euler’s formula and its proof using power series.
You will then dive into algebraic operations involving complex numbers, including addition, subtraction, multiplication, division, and finding the conjugate.
The course teaches you how to rationalize the denominator and perform division using different forms.
De Moivre’s formula is explained in detail, including its proof and applications in finding complex roots.
The syllabus covers solving equations involving complex roots for real unknowns and finding the nth root in different forms.
You will also learn to solve polynomial equations with complex roots.
The Argand diagram is utilized to visualize complex numbers and perform the four operations graphically.
Additionally, the course explores complex loci, which represent geometric shapes formed by complex numbers satisfying certain equations or conditions.
Basic concepts of Complex Numbers :Algebra of Complex Number
You’ll start with an introduction to iota and integral powers, learning through examples.
Then, you’ll dive into complex numbers themselves - understanding real and imaginary parts, equality, addition, subtraction, multiplication, division, conjugates, and modulus.
Plenty of examples are provided to reinforce your learning.
The course also covers important concepts like the square root of complex numbers and the cube root of unity, with multiple examples for each.
You’ll learn geometric representations of complex numbers and operations, including finding arguments.
Euler’s famous formula is explored in-depth.
Distance formulas, internal and external division formulas, and the equation of a circle are covered as well.
The powerful De Moivre’s Theorem is a key topic, with 10 examples walking you through its applications.
To test your knowledge, the course includes quizzes and practice sheets.
You’ll gain mastery over concepts like addition, multiplication, roots, geometric interpretations, and theorems like De Moivre’s.
Complex Numbers (AS/A Level, Edexcel/IGCSE/AQA/OCR)
The course starts by introducing imaginary numbers and the square root of -1, which is i.
You will learn about the powers of i and how to perform basic operations like addition, subtraction, multiplication, and division with complex numbers.
The course then dives into solving quadratic, cubic, and quartic equations with complex roots.
This is a crucial skill for advanced mathematics.
You will also explore the geometry of complex numbers using Argand diagrams, which are visual representations of complex numbers on a plane.
The course teaches you how to find the modulus (magnitude) and argument (angle) of complex numbers, as well as how to use vectors for addition and subtraction.
You will learn about the different forms of complex numbers and how to find the argument and modulus of products and quotients.
An important part of the course covers loci (paths) on the Argand diagram, including perpendicular bisectors, circles, and rays related to arguments.
You will study various regions on the Argand diagram defined by inequalities involving modulus and argument.
Throughout the course, you will work on interesting questions and applications related to loci, regions, and other complex number concepts.
This hands-on practice will solidify your understanding of the material.