Linear algebra is a fundamental branch of mathematics that deals with vectors, matrices, and systems of linear equations.
It’s a crucial foundation for fields like data science, machine learning, computer graphics, and more.
By mastering linear algebra, you gain the ability to solve complex problems, analyze data effectively, and create innovative solutions.
Finding a great linear algebra course on Coursera can be tricky, with so many options available.
You want a course that’s comprehensive, engaging, and taught by experts, but also fits your learning style and goals.
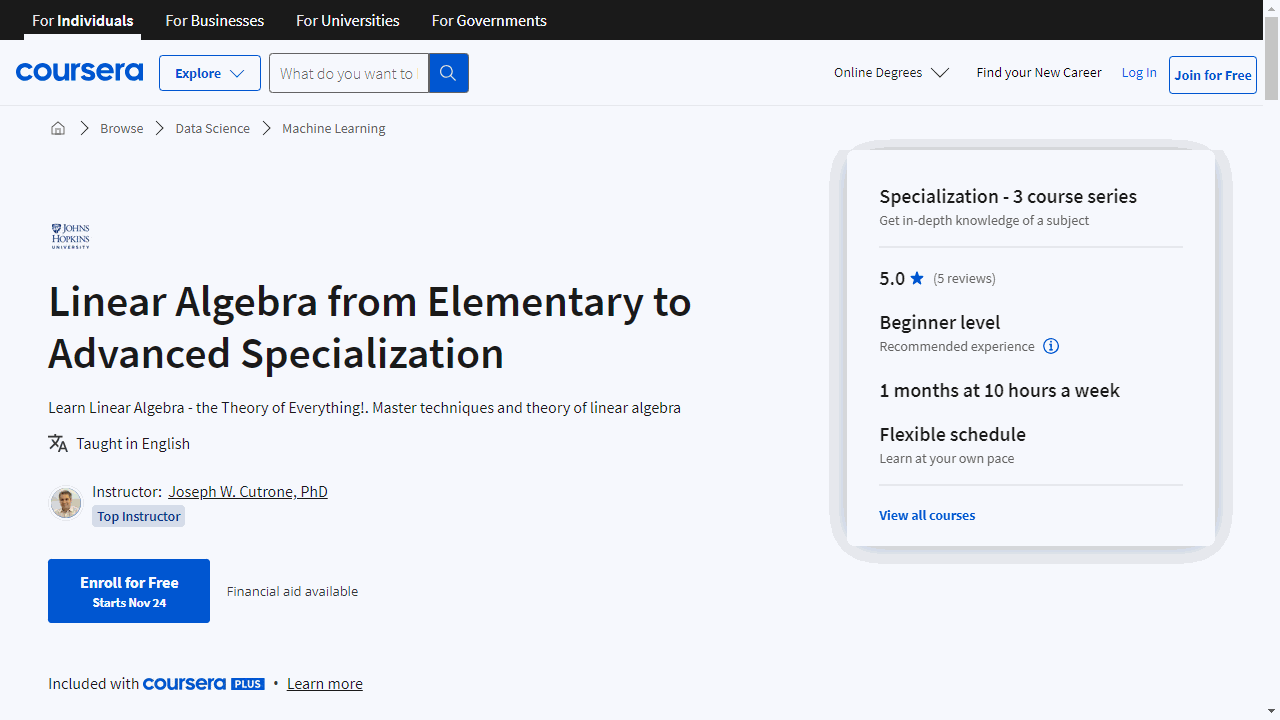
For the best linear algebra course overall on Coursera, we recommend the “Linear Algebra from Elementary to Advanced Specialization”.
This specialization covers all the fundamental concepts and provides a deep understanding of the subject.
It’s a fantastic choice for anyone looking to build a strong foundation in linear algebra, whether you’re just starting out or need to refresh your knowledge.
This is just one of many excellent linear algebra courses on Coursera.
Keep reading to explore more options for different learning levels and specific areas of interest, such as linear algebra for machine learning or data science.
Linear Algebra from Elementary to Advanced Specialization
This trio of courses is designed to build a robust foundation in linear algebra, a cornerstone of mathematics with practical applications across various fields.
The journey begins with “Linear Algebra: Linear Systems and Matrix Equations,” where you’ll delve into the essentials: linear equations, matrix operations, and analytical geometry.
More than just computational skills, this course emphasizes understanding the theoretical framework of linear algebra, enabling you to read and construct mathematical proofs.
By the end, you’ll have a firm grasp of the concepts needed to tackle linear systems.
Progressing to “Linear Algebra: Matrix Algebra, Determinants, & Eigenvectors,” you’ll deepen your understanding of matrices as functions that transform vectors.
This course hones your ability to manipulate matrices and introduces you to eigenvalues and eigenvectors, critical concepts with applications in data science and machine learning.
You’ll even explore real-world uses, such as the Google PageRank algorithm.
The final course, “Linear Algebra: Orthogonality and Diagonalization,” explores orthogonal vectors and transformations, leading to the study of symmetric matrices.
These concepts are particularly relevant to AI and machine learning, where matrix analysis is a fundamental component.
Completing this specialization equips you with the knowledge to pursue advanced studies in data science, AI, and mathematics.
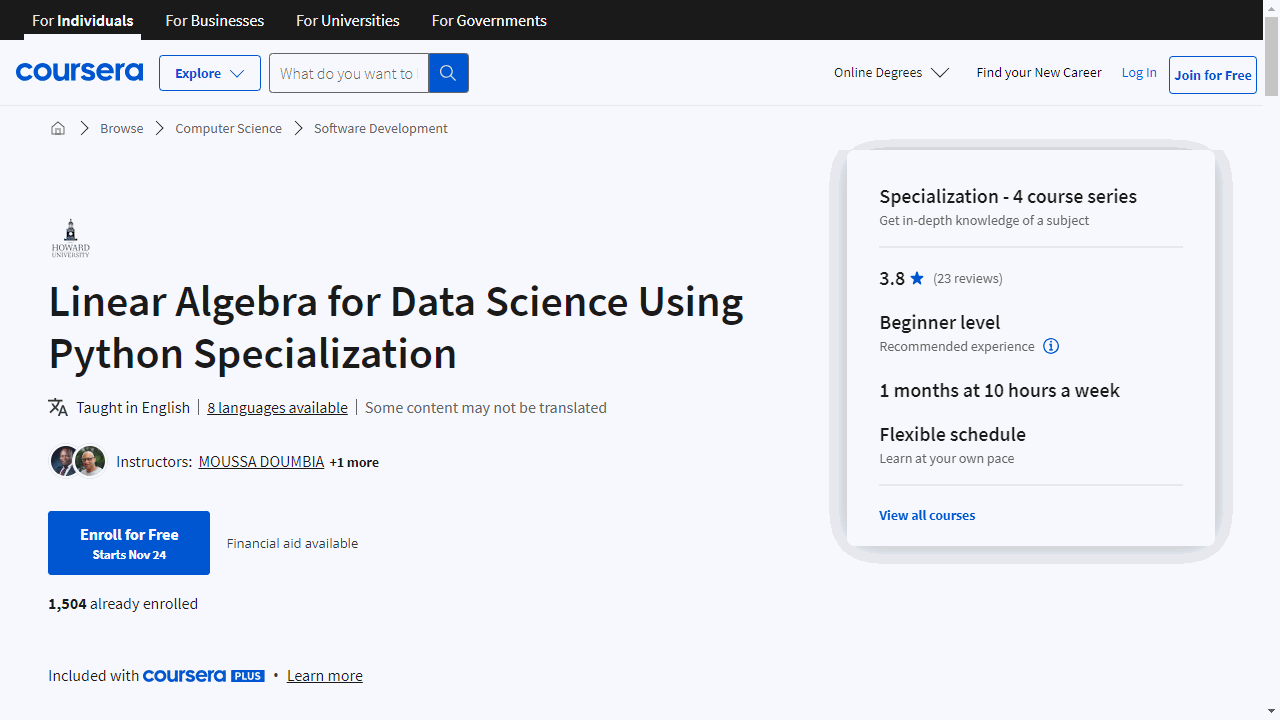
Linear Algebra for Data Science Using Python Specialization
This series is designed to equip you with the mathematical foundation and Python skills essential for a career in data science.
The journey begins with “Introduction to Linear Algebra and Python,” where you’ll grasp the essentials of linear algebra.
This course lays the groundwork with systems of linear equations, matrix operations, and vector equations, all while introducing you to Python, a critical tool for any data scientist.
Progressing to “Fundamental Linear Algebra Concepts with Python,” you’ll delve into more complex topics like matrix inverses and row reduction.
This course sharpens your problem-solving skills, enabling you to tackle linear transformations with confidence.
In “Building Regression Models with Linear Algebra,” the focus shifts to practical application.
You’ll explore various regression models, apply the Method of Least Squares, and harness Python to analyze and interpret data sets.
This course is where theory meets practice, giving you the ability to make data-driven decisions.
The specialization culminates with the “Capstone: Data Science Problem in Linear Algebra Framework,” where you’ll put your knowledge to the test.
You’ll develop and execute a regression model, then present your findings, showcasing your ability to solve real-world data science problems.
This specialization stands out for its balance of theoretical knowledge and practical application, all within the context of Python programming.
It’s a comprehensive learning path that not only teaches you linear algebra but also how to apply it directly to data science tasks.
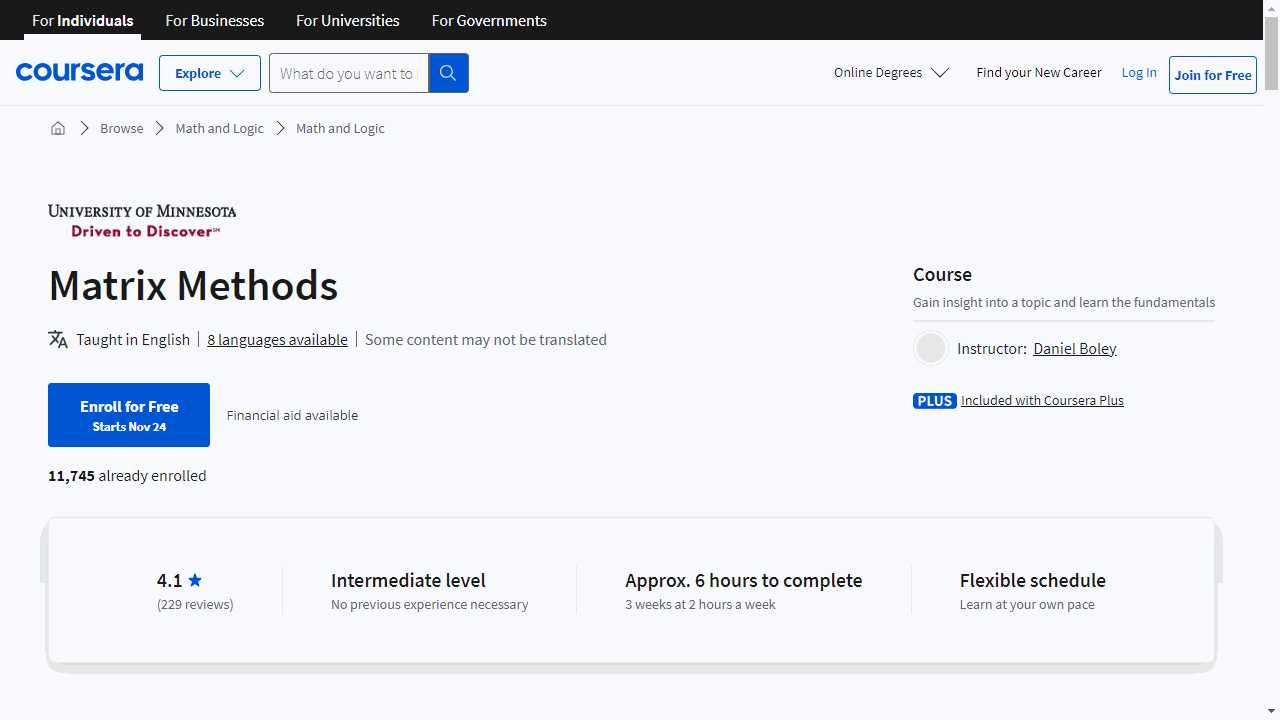
Matrix Methods
This course is a comprehensive journey through the essentials of matrices and linear equations, tailored to give you a robust understanding and practical skills.
You’ll begin with matrix operations, learning how to manipulate these numerical grids through multiplication—a foundational skill with vast applications.
The course doesn’t just stick to theory; it integrates Python and Numpy, providing you with hands-on experience in applying matrix concepts through coding.
Solving systems of linear equations is a core part of the curriculum.
You’ll master the elimination method, a strategic approach to uncovering unknown values, akin to solving a mathematical puzzle.
The course also demystifies LU Decomposition, breaking down complex matrices into simpler, more manageable components, streamlining the problem-solving process.
Orthogonality is another key topic, where you’ll explore the geometric principles of perpendicularity and their role in finding optimal solutions, such as in curve fitting scenarios.
This concept is crucial for understanding the inner workings of algorithms and data analysis.
Finally, the course delves into Singular Value Decomposition (SVD), a sophisticated technique with applications ranging from image processing to natural language processing.
SVD is a tool that can elevate your understanding of data structures and improve your ability to handle large-scale computational tasks.
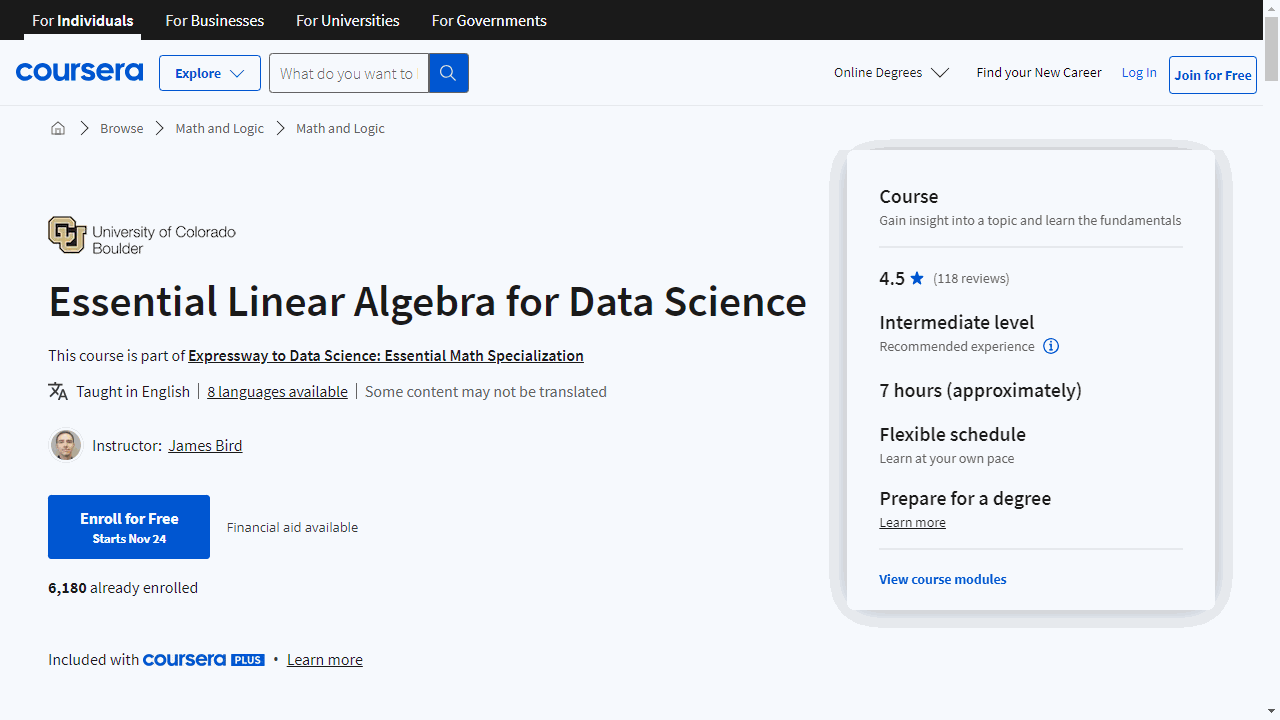
Essential Linear Algebra for Data Science
This course is structured to build your understanding from the ground up, starting with the fundamentals of linear systems and progressing to more complex concepts.
You’ll begin with an introduction that sets the stage for the entire course, ensuring you grasp the foundational elements of linear systems.
Visualization techniques will help you understand the solutions to these systems, providing a clear mental image of the concepts.
The transition from linear systems to matrices is seamless, with a focus on coefficient and augmented matrices.
You’ll learn to navigate through Gaussian Elimination (G.E.), a critical tool for solving linear equations, with a series of examples that illustrate single, infinite, and no-solution scenarios.
Matrix operations, including addition, scaling, and multiplication, are covered in detail.
The identity matrix is introduced, highlighting its pivotal role in matrix algebra.
You’ll also delve into vectors, learning how to manipulate them through linear combinations and understanding their span and reach.
Linear independence is another key topic, teaching you to recognize when vectors are unique and contribute distinct information.
This concept is vital in statistics, where redundancy can skew results.
The course then guides you through linear transformations and matrix inverses, equipping you with the skills to modify and control equations effectively.
Determinants are also explained, with step-by-step examples to solidify your understanding.
Eigenvalues and eigenvectors are demystified, showing their importance in transforming data analysis.
The course concludes with practical applications, such as least squares, which is essential for making sense of real-world data.
Linear Algebra for Machine Learning and Data Science
The course kicks off with the essentials, guiding you through systems of equations and the concept of singularity in matrices.
Understanding these principles is crucial—they’re the building blocks for more complex concepts you’ll encounter later on.
Determinants are next on the agenda, offering you a practical tool for assessing the solvability of equations.
You’ll get to grips with 2x2 and 3x3 systems, applying your knowledge to real-world scenarios.
The inclusion of NumPy Arrays introduces a practical element to your learning, bridging the gap between theory and application.
You’ll solve linear systems and visualize them, which is a vital skill in data science.
As you progress to week 1, you’ll delve into matrix row-reduction and the concept of rank, which reveals the potential solutions to a system.
This knowledge is pivotal for navigating complex data sets.
Week 2 focuses on vectors, their properties, and operations like dot products and scalar multiplication.
You’ll also explore matrices as linear transformations, a concept that’s fundamental to understanding algorithms in machine learning.
In week 3, the course deepens your understanding with eigenvalues and eigenvectors, unlocking the ability to decipher data patterns.
The concepts of bases and spans are introduced, expanding your mathematical toolkit.
Support is always at hand with a dedicated community forum, and additional resources like slides and troubleshooting tips ensure you have everything you need to succeed.
This course is a comprehensive, hands-on approach to linear algebra, designed to equip you with the skills necessary for a career in machine learning and data science.
Mathematics for Machine Learning: Linear Algebra
You’ll start with a clear introduction that outlines the importance of linear algebra in solving complex data problems.
The course swiftly moves to the essentials, teaching you about vectors—key components in the language of linear algebra—and how to manipulate them through various operations.
The curriculum is designed to be interactive, with real-world problems like the “apples and bananas problem” to help you grasp Gaussian elimination, a method for solving systems of equations.
You’ll also delve into matrix transformations, learning how they reshape space and can be combined for complex operations.
Special matrices are covered in detail, including orthogonal matrices and the Gram-Schmidt process, which simplifies vectors for easier computation.
These concepts are not just theoretical; they’re the tools that will sharpen your problem-solving skills in practical scenarios.
Eigenvectors and eigenvalues are introduced as the linchpins that unlock the deeper properties of matrices.
You’ll learn to calculate them and switch to the eigenbasis, simplifying complex matrix problems.
The course also touches on the PageRank algorithm, revealing the linear algebra behind search engine rankings.
Each module concludes with a summary to reinforce your learning, and additional resources are provided for those who wish to delve deeper.
The course’s structure ensures that you build a robust understanding of linear algebra, preparing you to apply these concepts confidently in machine learning contexts.
Also check our posts on: