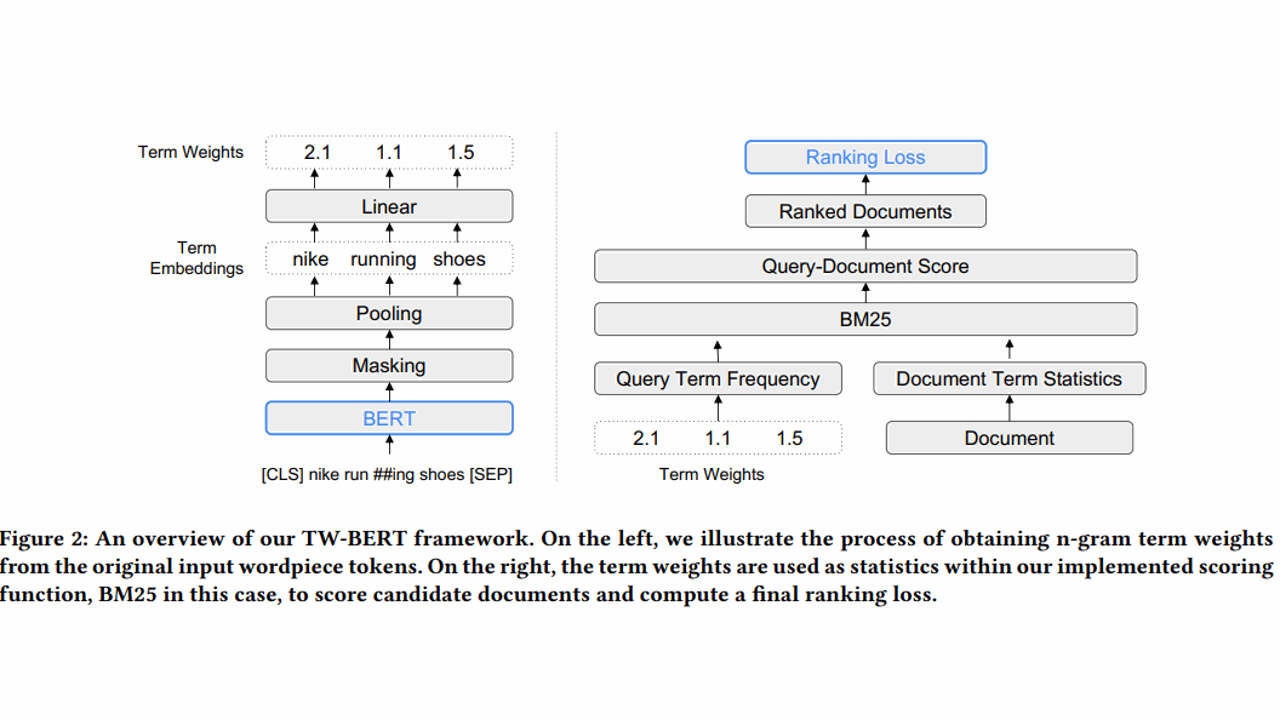
PyTorch Implementation of Google's TW-BERT for Information Retrieval

Information retrieval (IR) systems are crucial for a wide range of applications, from web search engines to personal digital assistants.

However, traditional IR systems can struggle with accurately understanding and ranking the relevance of documents based on user queries.

They typically rely on simple term-matching methods, known as sparse retrieval methods, that may not fully capture the semantic meanings of the terms in the queries.

While these methods are computationally efficient and easy to scale, they treat each term independently and fail to capture the contextual relationships between them.

The TW-BERT model by Google Research introduces a novel approach to this problem, using a BERT-based model, to infer the weights for n-grams in queries.

By combining deep learning models like BERT with traditional IR systems, the proposed method aims to improve the performance of first-stage Information Retrieval systems (candidate retrieval), where recall is the main objective.

This approach attempts to bridge the gap between the semantic richness of deep learning models and the scalability of sparse retrieval methods, potentially leading to more accurate and efficient IR systems.

Think about the query “apple third quarter earnings”.

While retrieving documents about “earnings” is important, we must rank the ones about “third quarter earnings” higher and, even more, the ones about “apple”.

Assigning higher weights to the terms “apple” and “third quarter” could help us achieve this.

The full implementation can be found here.

Initialization (`init` method)

The class TWBERT is defined as a subclass of torch.nn.Module, which is the base class for all neural network modules in PyTorch.

# Define the TW-BERT model as a subclass of PyTorch's base class for all neural network modules
class TWBERT(torch.nn.Module):
    def __init__(self):
        # Call the parent constructor
        super().__init__()
        
        # Load the pre-trained BERT model
        self.bert_model = AutoModel.from_pretrained("bert-base-uncased").base_model
        
        # Define the linear transformation to predict term weights
        self.linear = torch.nn.Linear(768, 1)
        
        # Define the ReLU activation function to ensure non-negative term weights
        self.relu = torch.nn.ReLU()

During initialization, the class creates three main components:

`self.bert_model`

This is the BERT model that is used to extract contextualized wordpiece embeddings.

The model is loaded using the from_pretrained method, which loads a pre-trained model given a model name or path.

In this case, it’s the "bert-base-uncased" model. The same used by the paper authors.

`self.linear` and `self.relu`

This is a linear transformation (fully connected layer) used to predict the term weights from the term-level embeddings.

The layer transforms multiple 768-dimensional inputs (the size of BERT’s hidden states for each wordpiece/n-gram) to a 1-dimensional output (the term weights).

For example, for the query “new york times”, the input to the linear layer would be a 3 x 768 tensor, where 3 is the number of n-grams in the query and 768 is the size of BERT’s hidden states.

The output would be a 3 x 1 tensor, where each element is the predicted term weight for the corresponding n-gram.

The ReLU (Rectified Linear Unit) activation function ensures that the predicted term weights are non-negative.

Forward pass (`forward` method)

This method describes how the input data flows through the network.

    def forward(self, input_ids, attention_mask, term_mask):
        # Obtain the hidden states of the wordpiece tokens from the BERT model
        bert_output = self.bert_model(input_ids, attention_mask=attention_mask).last_hidden_state # 1 x |W| x d
        
        # Expand the term mask along the last dimension to match the dimensions of the BERT output
        mask_ = term_mask.unsqueeze(-1) # |T| x |W| x 1

        # Perform element-wise multiplication of the BERT output and the term mask to mask out non-relevant wordpiece embeddings per n-gram term
        q_h_masked = bert_output * mask_ # |T| x |W| x d - Masking
        
        # Average the masked embeddings over the wordpiece dimension to obtain the term-level embeddings
        p = q_h_masked.mean(dim=1)  # |T| x d - Pooling
        
        # Pass the term-level embeddings through the linear layer and the ReLU activation to obtain the final term weights
        return self.relu(self.linear(p)) # |T|

`bert_output`

The BERT model is used to obtain the hidden states of the wordpiece tokens.

The last_hidden_state attribute is used, which returns the sequence of hidden states at the output of the last layer of the model.

`mask_`, `q_h_masked`, and `p`

The term mask is expanded along the last dimension to match the dimensions of bert_output.

The masked embeddings are averaged over the wordpiece dimension to obtain the term-level embeddings.

This is done using the mean function along the second dimension.

If the query “new york times” is broken into the following wordpieces: “new”, “york”, “ti”, “mes”, the mask will make sure that the embeddings for “ti” and “mes” are averaged together to obtain the term-level embedding for “times”.

The term-level embeddings are then passed through the linear layer and the ReLU activation function to obtain the final term weights.

The output of the forward pass is a tensor of term weights.

Fine-tuning Loss Function (`TWBERTLossFT` class)

This code defines a custom loss function for the TW-BERT model during the fine-tuning phase (Section 3.4.2).

The class TWBERTLossFT inherits from torch.nn.Module, which is the base class for all neural network modules in PyTorch.

class TWBERTLossFT(torch.nn.Module):
    def __init__(self, d1=0.2, d2=1):
        super().__init__()
        self.d1 = d1
        self.d2 = d2

In the constructor, d1 and d2 are hyperparameters for the loss function, which are set to 0.2 and 1 by default, and will be explained later.

The forward method defines the computation performed at every call. It takes two arguments: scores and labels.

scores are the predicted scores from the model and labels are the true relevance scores.

def forward(self, scores, labels):
    a_scores = torch.abs(scores - labels)

a_scores is the absolute difference between the predicted scores and true labels.

The next part of the code computes the adapted mean squared error (AMSE) loss as described in the paper.

This loss function is designed to be more robust when training on larger real-world datasets by avoiding small updates caused by noise in labels.

amse_loss = torch.zeros(scores.shape[0])
amse_loss = torch.where((a_scores >= self.d1) & (a_scores < self.d2), 
                0.5 * (scores - labels)**2, amse_loss)
amse_loss = torch.where(a_scores >= self.d2, self.d2 * (a_scores - 0.5 * self.d2), amse_loss)

The torch.where function is used to apply different loss calculations based on the value of a_scores.

If the absolute difference is between d1 and d2, the standard mean squared error is applied. If it’s greater than d2, a Huber loss is applied which reduces the penalty for large errors.

The next part of the code is used to compute the ListMLE loss, a list-wise ranking loss.

I adapted it borrowing code from the repository linked above.

This is used as an additional signal to correctly order the scores.

random_indices = torch.randperm(scores.shape[-1])
y_pred_shuffled = scores[random_indices]
y_true_shuffled = labels[random_indices]

y_true_sorted, indices = y_true_shuffled.sort(descending=True, dim=-1)

preds_sorted_by_true = y_pred_shuffled[indices]

max_pred_values, _ = preds_sorted_by_true.max(dim=0, keepdim=True)

preds_sorted_by_true_minus_max = preds_sorted_by_true - max_pred_values

cumsums = torch.cumsum(preds_sorted_by_true_minus_max.exp().flip([0]), 0).flip([0])

observation_loss = torch.log(cumsums + DEFAULT_EPS) - preds_sorted_by_true_minus_max

Here, the predicted scores and true labels are shuffled with the same random permutation.

Then, the shuffled labels are sorted in descending order and the predicted scores are rearranged accordingly.

These scores are then normalized by subtracting the maximum predicted score.

The cumulative sum of the exponentiated normalized scores is computed in reverse order.

The observation loss is then computed as the log of the cumulative sums minus the normalized scores.

The final line of the method returns a sum of the means of the AMSE loss and the ListMLE loss.

return amse_loss.mean() + observation_loss.mean()

Building The Mask To Weight The Query Terms (`token_and_mask_query` function)

This function, token_and_mask_query, tokenizes a given query and creates a mask for the terms in that query (Section 3.1).

It’s done because BERT outputs wordpiece embeddings, but the TW-BERT model needs term-level embeddings, so we map the wordpiece embeddings to n-grams by averaging the wordpiece embeddings for each term.

The function takes two arguments: query, which is the text of the query, and tokenizer, which is a tokenizer object from the transformers library.

def token_and_mask_query(query, tokenizer):
    query_t = tokenizer(query, return_tensors="pt", padding=True)

The tokenizer is used to convert the query into tokens.

The return_tensors argument is set to "pt" to return PyTorch tensors, and padding=True ensures that all the returned tensors have the same length by adding padding tokens if necessary.

ngrams = re.findall(r"[a-z0-9']+", query)

The re.findall function is used with a regular expression to find all n-grams in the query.

In this case, an n-gram is defined as a sequence of alphanumeric characters or apostrophes.

term_t = [tokenizer(ng, add_special_tokens=False).input_ids for ng in ngrams]

Each n-gram is then tokenized without adding special tokens (SEP and CLS), and their input IDs are stored in the term_t list.

mask = torch.zeros(len(ngrams)+2, query_t["input_ids"].shape[1])

A mask tensor is created with the same number of rows as the number of n-grams plus two (to account for the special tokens on BERT’s output), and the same number of columns as there are tokens in the query.

for i in range(1,len(ngrams)+1):
    for j in term_t[i-1]:
        mask[i, query_t["input_ids"][0] == j] = 1

The mask is then filled in such a way that for each n-gram, the positions of its tokens in the query are marked with a 1.

return query_t, mask

Finally, the function returns the tokenized query and the mask tensor.

Internal BM25 Scoring Function (`score_vec` function)

This function, score_vec, calculates the BM25 scores for a query against a corpus of documents (Section 3.2).

It takes as input a query, a term frequency vector for the query, the corpus of documents (candidates), term weights for the query, the average document length, and the BM25 parameters k1, k3, and b.

def score_vec(query, query_tf_vec, corpus, term_weights, avg_doc_len, k1=1.2, k3=8., b=0.75):

The query is a string, query_tf_vec is a vector of term frequencies for the query, corpus is a list of documents where each document is represented as a dictionary of term frequencies, term_weights is a tensor of term weights for the query (output of TW-BERT), and avg_doc_len is the average document length in the corpus.

query = re.findall(r"[a-z0-9']+", query)
f_ti_t_w = term_weights * query_tf_vec
num_docs = len(corpus)

The query is split into terms using a regular expression.

The term frequency vector for the query is element-wise multiplied with the term weights to get f_ti_t_w.

The number of documents in the corpus is stored in num_docs.

query_idf = {}
for term in query:
    df_t = sum([1 for doc_tf in corpus if term in doc_tf])
    query_idf[term] = math.log((num_docs - df_t + 0.5)/(df_t+0.5) + 1)

The inverse document frequency (IDF) for each term in the query is calculated and stored in query_idf.

The IDF is calculated as the logarithm of the number of documents divided by the document frequency of the term, with some adjustments to avoid division by zero.

doc_scores = list()
for doc_tf in corpus:
    doc_len = sum(doc_tf.values())
    doc_tf_vec = torch.Tensor([doc_tf[term] for term in query])
    num = doc_tf_vec * (k3 + 1) * f_ti_t_w
    k = k1 * ((1-b) + b * doc_len/avg_doc_len) + doc_tf_vec
    den = (k3 + f_ti_t_w) * k
    idf = torch.Tensor([query_idf[term] for term in query])
    doc_scores.append(torch.sum(idf * num/den))

For each document in the corpus, the BM25 score for the document against the query is calculated and appended to doc_scores.

The BM25 score is calculated as the sum of the IDF times the numerator divided by the denominator for each term in the query.

The numerator is the term frequency in the document times (k3 + 1) times f_ti_t_w, which is the term weight times the term frequency in the query.

The denominator is (k3 + f_ti_t_w) times k, where k is k1 times a normalization factor plus the term frequency in the document.

return torch.stack(doc_scores)

Finally, the function returns a tensor of document scores by stacking the list of scores.

This tensor can be used to rank the documents in the corpus according to their relevance to the query.

Differences From The Original Paper

No Bi-gram: This implementation does not consider bi-grams (two-word phrases) when assigning term weights. The original paper’s model consider both uni-grams (single words) and bi-grams.
No Query Expansion: Query expansion, a technique used to improve retrieval performance by adding synonyms or related terms to the original query, is not used in this implementation.
Term Uniqueness: The original paper is unclear on whether it uses unique terms or all terms in the query for the term weighting process. This implementation uses the original query with all terms.
No Score Normalization: This implementation does not implement the score normalization process described in the original paper.
Pretraining: The original paper may use a pretraining phase, where the model is trained on a large, general dataset before being fine-tuned on the specific task. The BERT model used is pretrained, but not on the MSMARCO dataset with T5 query expansion.

Initialization (__init__ method)#

self.bert_model#

self.linear and self.relu#

Forward pass (forward method)#

bert_output#

mask_, q_h_masked, and p#

Fine-tuning Loss Function (TWBERTLossFT class)#

Building The Mask To Weight The Query Terms (token_and_mask_query function)#

Internal BM25 Scoring Function (score_vec function)#

Differences From The Original Paper#