Mathematics is the language of science and technology, a fundamental tool for understanding the world around us and solving complex problems.
From data analysis and machine learning to engineering and finance, a strong mathematical foundation is invaluable for a wide range of fields.
Learning mathematics can unlock new avenues for problem-solving, analytical thinking, and critical reasoning.
Finding the right mathematics course on Coursera can be a daunting task, given the sheer number of options available.
You’re looking for a program that’s engaging, comprehensive, and taught by experts, but also fits your learning style and goals.
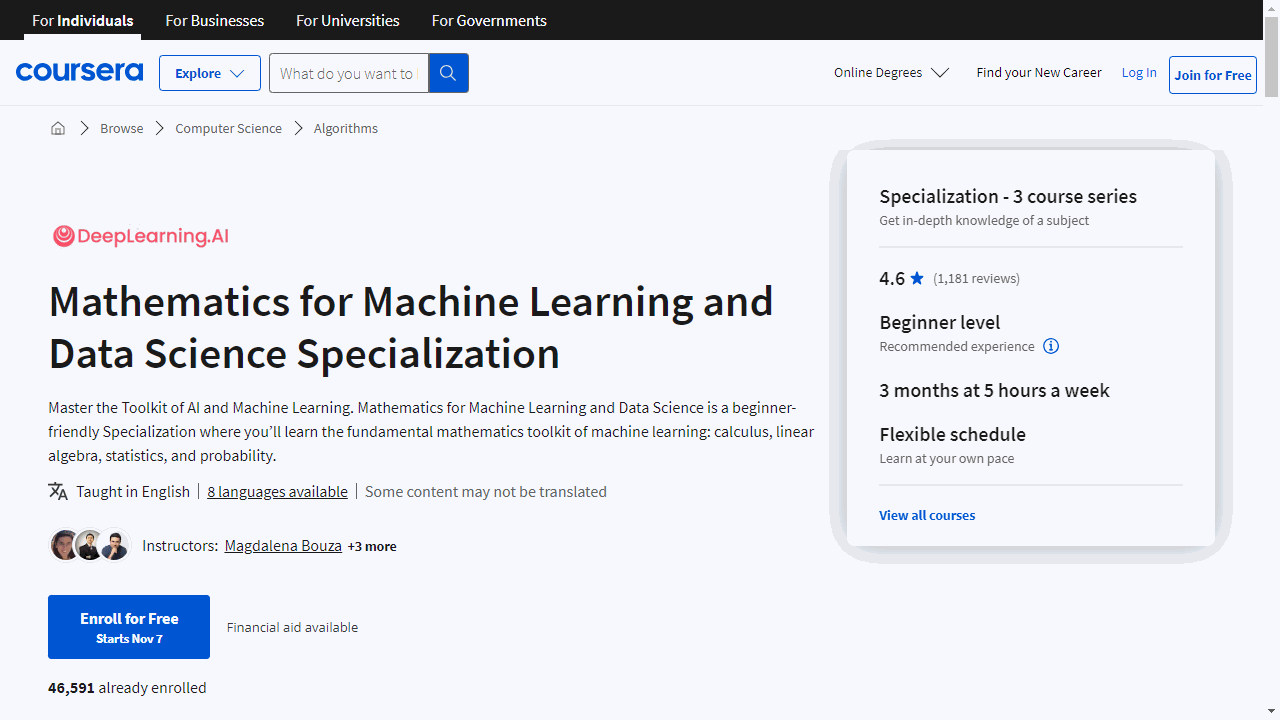
For the best mathematics course overall on Coursera, we recommend the Mathematics for Machine Learning and Data Science Specialization.
This specialization is a trio of courses designed to equip learners with the mathematical skills essential for succeeding in machine learning and data science.
From linear algebra and calculus to probability and statistics, the courses provide a comprehensive foundation in the core concepts needed to understand and implement machine learning algorithms.
This is just the tip of the iceberg when it comes to quality mathematics courses on Coursera.
Keep reading to explore our recommendations for different learning styles and goals, including courses tailored for specific areas of mathematics, such as calculus, linear algebra, or discrete mathematics.
We also have recommendations for courses that focus on the application of mathematics in specific fields, like engineering, economics, or computer science.
Mathematics for Machine Learning and Data Science Specialization
This is a trio of courses tailor-made to turn you into a math-savvy machine learning enthusiast.
First up, “Linear Algebra for Machine Learning and Data Science” is where data becomes more than just numbers.
You’ll learn to represent data in ways that computers love—through vectors and matrices.
This isn’t just about crunching numbers; it’s about understanding the properties that make algorithms tick.
You’ll conquer operations like the dot product and determinants, and unlock the power of eigenvalues and eigenvectors to solve complex problems with ease.
Next, “Calculus for Machine Learning and Data Science” is your playground for optimization.
This course demystifies how to fine-tune functions to get the best out of your machine learning models.
You’ll get hands-on with derivatives and gradients, and explore the inner workings of neural networks through gradient descent.
Then there’s “Probability & Statistics for Machine Learning & Data Science,” where you’ll tackle the uncertainties of predictions head-on.
You’ll get comfortable with probability distributions and learn how to use statistical methods. From interval estimates to hypothesis testing, you’ll gain the confidence to assess and improve model performance.
This specialization is crafted with beginners in mind, so don’t worry if you’re not a math whiz yet. With a foundation in high school math and a sprinkle of Python, you’ll be set to start. The courses are filled with intuitive explanations and visual aids that make complex concepts accessible.
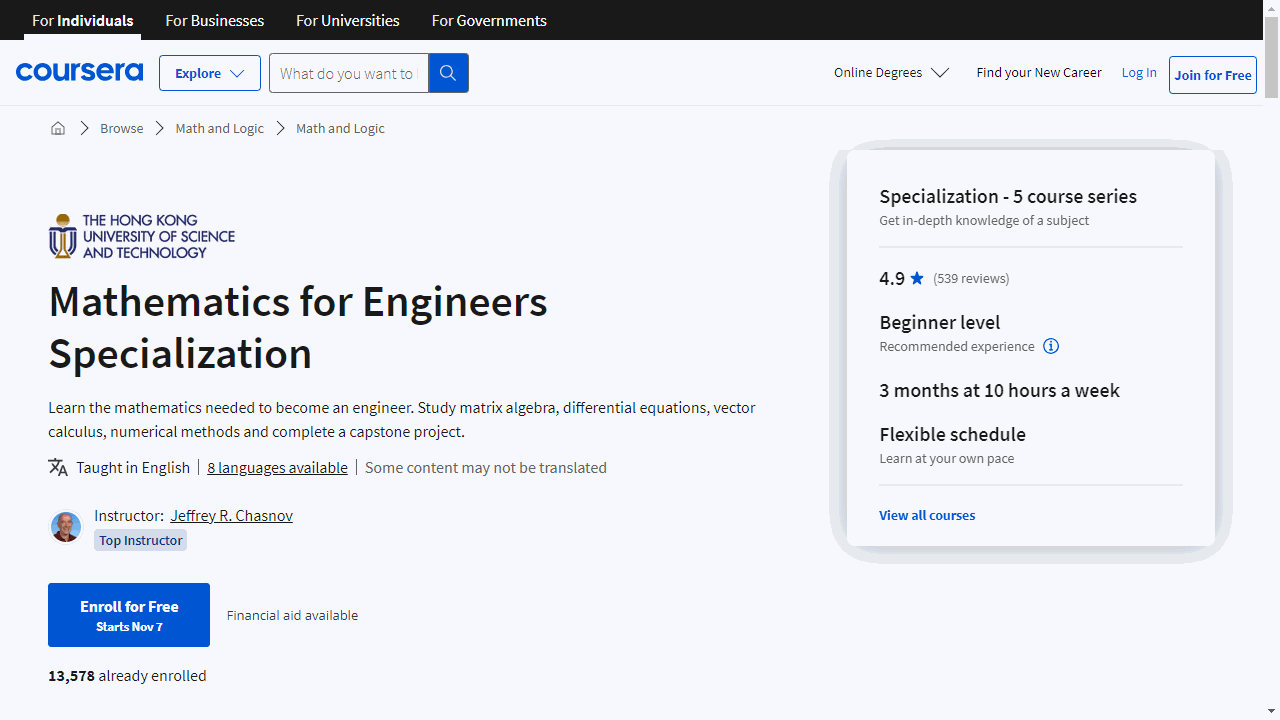
Mathematics for Engineers Specialization
If you’re searching for top-notch math courses tailored for engineers, the “Mathematics for Engineers Specialization” on Coursera is a solid choice.
Each course is designed to build on your knowledge and apply it to real-world engineering challenges.
Starting with “Matrix Algebra for Engineers,” you’ll delve into the essentials of matrices, a foundational tool in engineering problem-solving.
The course is structured with concise videos, complemented by problem sets and quizzes to reinforce your learning.
By the end of the four-week course, you’ll have a firm grasp on linear equations, vector spaces, and the key concepts of eigenvalues and eigenvectors.
Moving on to “Differential Equations for Engineers,” you’ll explore the theories and applications of differential equations.
Over six weeks, you’ll progress from first-order to partial differential equations, equipping you with the skills to model and analyze dynamic systems.
“Vector Calculus for Engineers” expands your calculus toolkit into multiple dimensions, crucial for fields like electromagnetism and fluid mechanics.
You’ll learn about vector fields, multivariable integration, and the pivotal theorems of vector calculus.
“Numerical Methods for Engineers” introduces you to the numerical techniques essential in engineering analysis.
This course emphasizes practical application, teaching you to use MATLAB to solve numerical problems. By the end, you’ll be adept at using computational tools to tackle complex engineering tasks.
The specialization culminates with “Mathematics for Engineers: The Capstone Course,” where you’ll apply your accumulated knowledge to a project in computational fluid dynamics.
This hands-on experience is a chance to solidify your skills and demonstrate your ability to solve engineering problems using MATLAB.
The structure of the courses—with regular quizzes and problem sets—ensures that you can track your progress and solidify your understanding as you go.
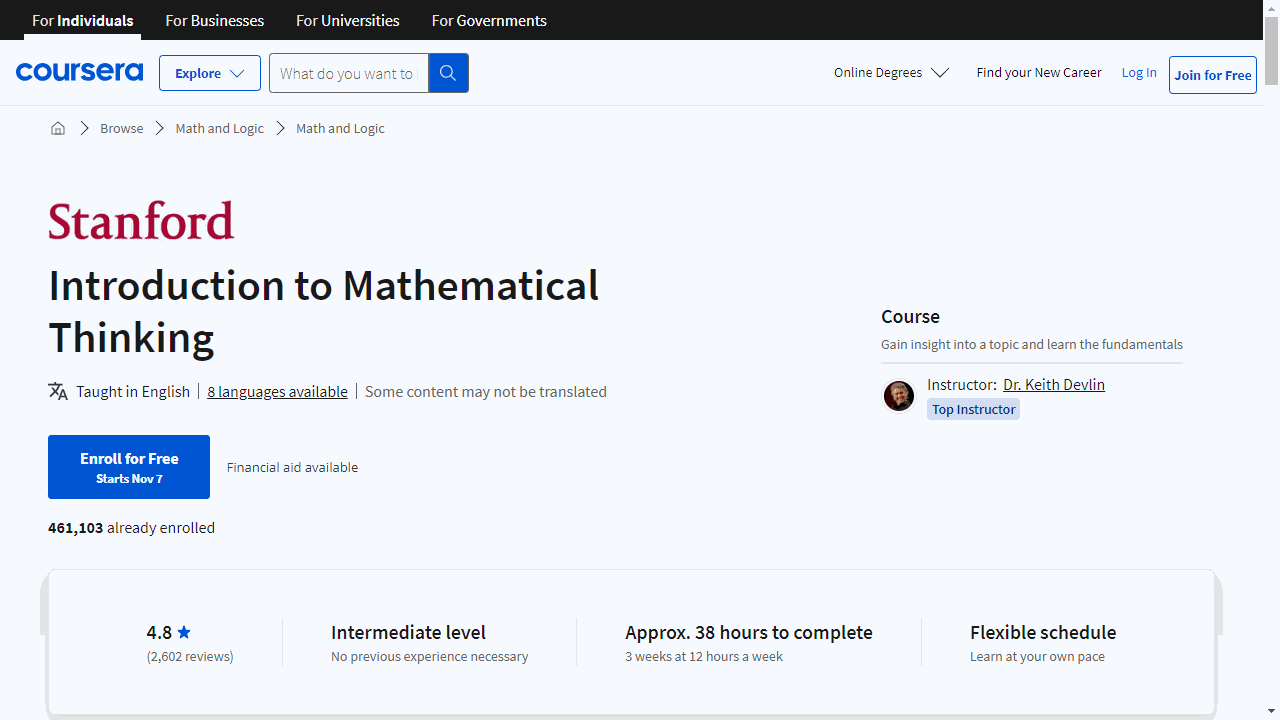
Introduction to Mathematical Thinking
If you’re searching for a math course that goes beyond the usual formulas and equations, “Introduction to Mathematical Thinking” might be just what you need. This course is designed to reshape your approach to mathematics, focusing on the thought process rather than just the solutions.
Keith Devlin, a renowned mathematician from Stanford, guides you through the course with a series of engaging lectures.
The course begins with a welcoming introduction, setting a friendly tone and preparing you for the journey ahead. In Lecture 1, you’ll get a taste of what mathematical thinking entails, laying a solid foundation for the more complex topics to come.
Lecture 2 delves into Logical Combinators, teaching you how to build intricate statements from simpler ones. It’s like learning a new language within mathematics. The accompanying assignments and tutorials ensure that you’re not just passively learning but actively engaging with the material.
As you progress to Lectures 3 and 4, you’ll tackle Implication and Equivalence, two pillars of logical reasoning. These concepts are crucial for developing a rigorous mathematical mindset. The course also includes a helpful supplement on how to use the evaluation rubric, giving you clear insights into your progress and areas for improvement.
Quantifiers are introduced in Lecture 5, adding depth to your understanding of mathematical statements. And if you’re worried about deciphering complex formulas, the course provides a supplement specifically designed to help you read and interpret mathematical expressions with ease.
The heart of the course lies in constructing proofs, covered in Lectures 7 and 8. Here, you’ll learn to piece together logical arguments, a skill that’s central to all of mathematics. It’s akin to solving a puzzle, where each piece is a logical step leading to a satisfying conclusion.
Number Theory and Real Analysis are explored in later lectures, where you’ll discover the elegance and applications of these fields. These sections of the course reveal the interconnectedness of mathematical concepts and their relevance to real-world phenomena.
Throughout the course, a series of tutorials and problem sets provide a practical framework for applying what you’ve learned. These exercises are thoughtfully crafted to reinforce your understanding and build confidence in your new skills.
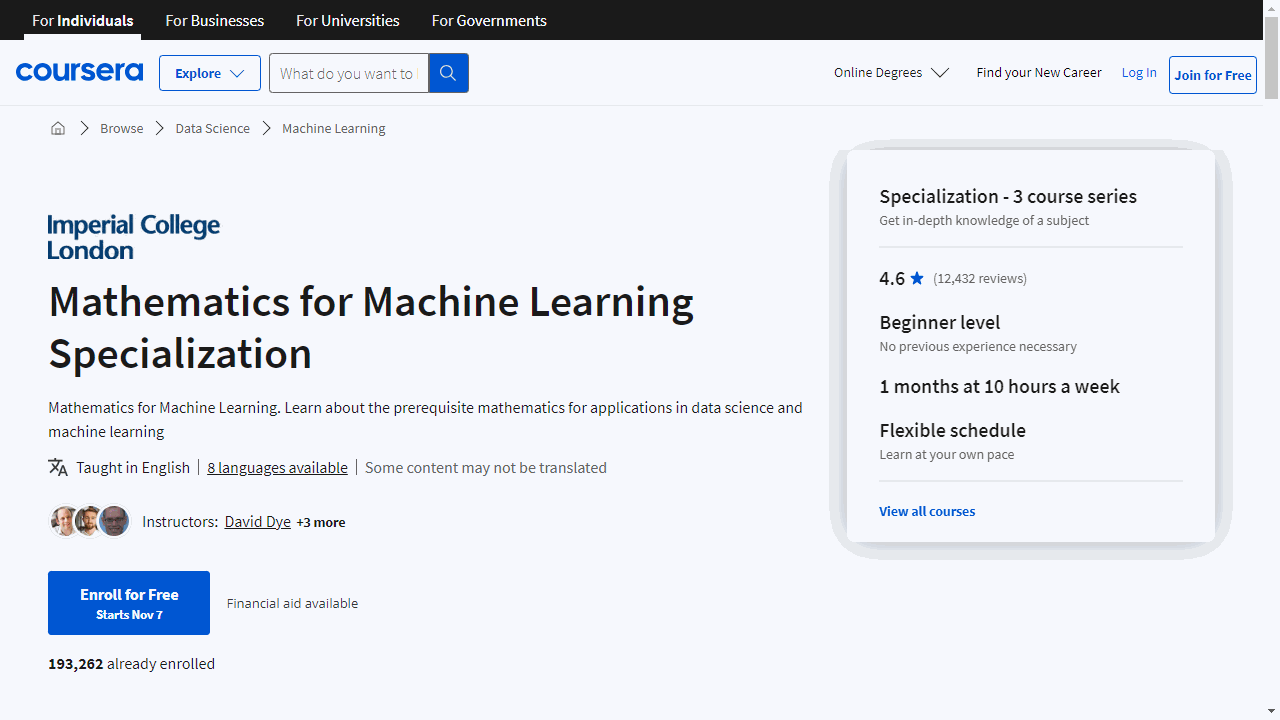
Mathematics for Machine Learning Specialization
This specialization is another alternative if your goal is to learn math to tackle machine learning and data science challenges.
Let’s kick things off with “Mathematics for Machine Learning: Linear Algebra.”
Imagine linear algebra as the foundation of a towering skyscraper. This course is your blueprint, guiding you through the essentials of vectors and matrices.
You’ll unravel the complexities of eigenvalues and eigenvectors, and apply these concepts to real-world scenarios, like spinning images and exploring algorithms behind search engines.
And don’t worry about getting your hands dirty with code – this course has you covered with bite-sized Python exercises, perfect for beginners and a great refresher for seasoned coders.
Moving on to “Mathematics for Machine Learning: Multivariate Calculus.”
Starting from the ground up, you’ll revisit the concept of slope and quickly ascend to mastering gradients.
This course isn’t just about watching numbers on a screen; you’ll engage in interactive games that make calculus both fun and memorable.
By the end, you’ll be equipped with an intuitive understanding of calculus, ready to decode more complex machine learning courses with ease.
Finally, “Mathematics for Machine Learning: PCA.”
You’ll dive into statistics, play with inner products, and project data onto lower-dimensional spaces.
This course is hands-on, with Jupyter notebooks that let you practice PCA (Principal Component Analysis) on real datasets.
It’s a bit more challenging, with a focus on abstract thinking and programming, but it’s the kind of challenge that primes you for the real world of machine learning algorithms.
Precalculus through Data and Modelling Specialization
This series of courses is designed to equip you with the mathematical tools you need to interpret and understand the world around you, making it ideal for anyone with a curiosity for how things work, not just math enthusiasts.
The first course in the series, “Precalculus: Relations and Functions,” lays a solid foundation.
Here, you’ll explore the concept of functions, which are essential for modeling and analyzing real-world data.
You’ll engage with actual data sets, using functions to uncover patterns and insights that are applicable across various fields, from natural sciences to sociology.
Moving on to “Precalculus: Periodic Functions,” you’ll delve into the rhythmic aspects of the world.
This course demystifies the mathematics behind cycles and oscillations that you encounter daily, from the ebb and flow of ocean tides to the fluctuations in the stock market.
By understanding periodic functions, you’ll gain a new perspective on the predictable patterns that govern many natural and man-made systems.
Lastly, “Precalculus: Mathematical Modeling” offers a hands-on approach to turning real-life challenges into solvable mathematical problems.
This course emphasizes the practical application of precalculus concepts, teaching you to construct and manipulate mathematical models.
You’ll work with vectors to navigate through space and quantities, an invaluable skill for fields as diverse as engineering and economics.
Each course in the specialization is crafted to be accessible, with a focus on visualization and technology to enhance your learning experience.
You’ll find the content reinforced through interactive exercises and regular assessments, ensuring that you’re not just passively absorbing information but actively mastering the material.
Differential Calculus through Data and Modeling Specialization
If you’re searching for a comprehensive math course that seamlessly blends theoretical calculus with practical application, the “Differential Calculus through Data and Modeling Specialization” on Coursera is exactly what you need.
This series of courses is designed to not only build your mathematical foundation but also to demonstrate how these concepts are vital in analyzing real-world data.
Starting with “Calculus through Data & Modeling: Precalculus Review,” you’ll revisit essential functions, including polynomial and trigonometric, with a twist. The course emphasizes using these functions for data modeling, offering a more engaging approach to precalculus.
The integration of technology, such as graphing calculators and computer software, ensures that you’re learning with the tools that are used in actual data analysis.
As you progress to “Calculus through Data & Modeling: Limits & Derivatives,” the course introduces the concept of limits to define derivatives.
This is where calculus begins to unveil its true potential, allowing you to understand how changes in one variable affect another - a fundamental skill in many scientific, financial, and engineering fields.
The journey continues with “Calculus through Data & Modeling: Differentiation Rules,” where you’ll learn shortcuts to finding derivatives.
This course simplifies complex calculations, making it easier to tackle a wide range of functions. By the end of this course, you’ll be equipped to solve problems involving rates of change and function approximation with confidence.
Lastly, “Calculus through Data & Modeling: Applying Differentiation” takes these concepts further by teaching you how to apply derivatives to graph analysis and optimization problems.
This course is particularly relevant as it touches on topics like machine learning and economic efficiency, showcasing the versatility of calculus in various professional contexts.
Each course in the Specialization builds on the last, ensuring a smooth transition from fundamental concepts to advanced applications. By the end, you’ll have a solid grasp of calculus principles and how they can be employed to interpret and solve real-world challenges.
Introduction to Discrete Mathematics for Computer Science Specialization
This suite of courses is designed to equip you with the mathematical tools and concepts essential for a career in computer science.
The specialization kicks off with “Mathematical Thinking in Computer Science,” which lays the foundation for logical reasoning and problem-solving.
You’ll explore induction, recursion, and logic through interactive puzzles that encourage hands-on learning. The course is accessible even if your math skills are just at the basic level, but you’ll need some Python knowledge for the programming quizzes.
Moving on to “Combinatorics and Probability,” you’ll delve into efficient counting methods and develop a practical understanding of probability. This course is particularly relevant if you are interested in algorithms and data analysis, culminating in a project where you’ll program a strategy for a dice game.
For a visually engaging experience, “Introduction to Graph Theory” introduces you to the concepts that underpin everything from social network analysis to operational logistics. You’ll appreciate the real-world applications as you work on algorithms that have significant implications in various industries.
In “Number Theory and Cryptography,” you’ll uncover the relationship between abstract mathematics and practical encryption techniques. This course demystifies the principles behind secure online communication, providing you with the skills to encrypt and decrypt messages.
Finally, “Delivery Problem” challenges you to apply your newfound knowledge to the travelling salesman problem, a classic dilemma in computer science. You’ll experiment with different algorithms and learn how discrete mathematics can lead to more efficient solutions.
You’ll gain valuable skills in probability, combinatorics, number theory, and cryptography.
Algebra: Elementary to Advanced Specialization
Starting with “Algebra: Elementary to Advanced - Equations & Inequalities,” you’ll establish a foundational grasp of algebra that’s essential for any further mathematical study.
This course covers the essentials, from the real number system to quadratic equations, and emphasizes the application of these concepts to real-world scenarios. It’s an excellent starting point for ensuring your computational methods are up to par and that you’re comfortable with algebraic formulas and properties.
Moving on to “Algebra: Elementary to Advanced - Functions & Applications,” the course shifts focus to the concept of functions, a cornerstone in algebra.
You’ll learn to identify and apply various types of functions, understanding their domains, ranges, and graphs. This course aims to enhance your problem-solving abilities by teaching you to analyze functions both algebraically and analytically, preparing you to tackle real-world problems with a strong mathematical approach.
The final course, “Algebra: Elementary to Advanced - Polynomials and Roots,” delves into more complex algebraic topics. It’s designed to refine your analytical skills, enabling you to make logical deductions and informed conclusions.
This course is particularly valuable for those planning to advance to calculus, statistics, or data science, as it focuses on the quantitative skills needed for evaluating arguments and making predictions.
By the end of the specialization, you’ll have a comprehensive set of algebra skills that are applicable to both academic pursuits and real-world problem-solving.
Game Theory
This course isn’t just about numbers; it’s a journey into the decision-making processes that shape competition and cooperation in various aspects of life.
The course kicks off with an engaging introduction to Game Theory, using the example of TCP Backoff—a protocol that governs internet traffic—to illustrate complex concepts in a relatable way.
This sets the stage for exploring the motivations and actions of self-interested agents, a foundational element in understanding how and why decisions are made.
As you progress, you’ll learn to define and identify different types of games.
Real-world examples bring these concepts to life, demonstrating the practical applications of Game Theory in economics, politics, and beyond.
The course then introduces the Nash Equilibrium, a cornerstone of Game Theory that reveals how individuals or groups reach a state where no one benefits from changing their strategy.
You’ll also explore mixed strategies, which add a layer of unpredictability to decision-making.
This section is particularly insightful, as it includes data from professional sports to show how these theories play out on the field.
The instructor then takes you beyond the basics, addressing more complex scenarios such as games with changing rules or incomplete information.
These lessons are crucial for understanding strategic thinking in dynamic environments.
In the latter modules, the course delves into repeated and coalitional games, where long-term strategy and group dynamics come into play.
You’ll learn about concepts like the Shapley value and the Core, which help determine the contributions and payoffs for individuals within a group.
This course is a deep dive into the mechanics of strategic thinking, offering insights that are applicable well beyond the realm of mathematics.
If you’re ready to think critically and elevate your problem-solving skills, this course is your next smart move.
Introduction to Complex Analysis
If you’re searching for a math course that offers both depth and breadth, the “Introduction to Complex Analysis” course is a great choice.
This course is an exploration of mathematical concepts that are foundational to advanced mathematics and physics.
The journey begins with the history of complex numbers, providing context that enriches your understanding of their role in modern math.
From there, you’ll delve into the algebra and geometry of the complex plane, which is essential for visualizing and solving complex problems.
Polar representation and the roots of complex numbers come next, offering a new perspective on the magnitude and direction of these numbers.
This section is particularly useful for visual learners, as it introduces a graphical approach to complex numbers.
Topology in the plane may sound intimidating, but it’s a fascinating topic that examines the properties of space that are preserved under continuous transformations.
It’s like learning the rules of a game that shapes the universe.
The course also covers complex functions, sequences, and limits, which are the building blocks for understanding more advanced concepts.
You’ll appreciate the beauty of patterns in mathematics as you study Julia Sets and the Mandelbrot Set, which are not only visually stunning but also illustrate the complexity within simple equations.
Technical skills are developed through lessons on the complex derivative and the Cauchy-Riemann equations, which are crucial for anyone looking to delve deeper into engineering or physics.
The complex exponential and trigonometric functions expand your toolkit, allowing you to solve a wider range of problems.
Analytic functions are a major focus, and you’ll learn about their properties and how to work with inverse functions.
Conformal mappings and Möbius transformations will challenge you to think about shapes and spaces in innovative ways.
The Riemann Mapping Theorem and complex integration are covered comprehensively, ensuring you have a solid grasp of these essential concepts.
The course also introduces you to the implications of Cauchy’s Theorem, which is a cornerstone of complex analysis.
As you progress, you’ll encounter infinite series and power series, leading up to discussions on the Riemann Zeta Function and the Prime Number Theorem—topics that are at the heart of some of the most intriguing questions in mathematics.
The course concludes with a deep dive into Laurent Series, isolated singularities, and the Residue Theorem, equipping you with the skills to tackle complex integrals and apply these concepts in practical scenarios.
This course is an excellent choice for anyone serious about mathematics, whether you’re a student looking to supplement your studies or a lifelong learner driven by curiosity.