Optimization is the art and science of finding the best solution to a problem, given constraints and objectives.
It’s a powerful tool used in many industries like finance, logistics, and manufacturing, and mastering it can lead to significant improvements in efficiency and performance.
You might be looking for a course that covers specific optimization techniques or a broader approach to problem-solving.
Maybe you’re seeking a practical application of your knowledge or a deep dive into the theory.
Whatever your needs, finding the right course can feel overwhelming with so many options available.
We’ve looked at the best optimization courses on Coursera and narrowed it down to our top picks.
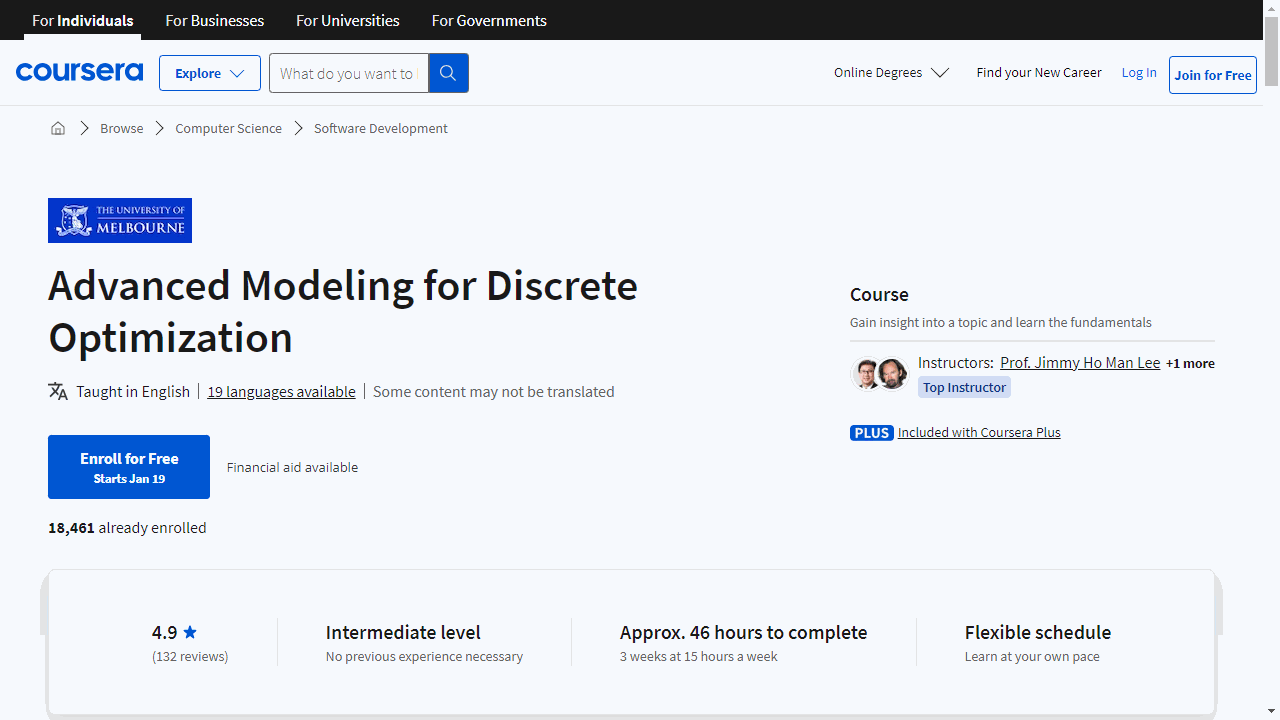
For the best optimization course overall, we recommend Advanced Modeling for Discrete Optimization by The University of Melbourne.
This course excels at providing a comprehensive overview of advanced modeling techniques and equips you with the skills to tackle complex problems.
You’ll delve into relational semantics, model debugging, and symmetry analysis, all within a hands-on learning environment using the industry-standard MiniZinc tool.
If this course doesn’t quite suit your needs, we have plenty of other options.
Keep reading for more recommendations for beginners, intermediate learners, and experts, as well as courses focusing on specific optimization techniques, algorithms, and applications.
Advanced Modeling for Discrete Optimization
Provider: The University of Melbourne
This course dives deep into optimization techniques, equipping you with the skills to tackle complex problems efficiently.
You’ll start by mastering model debugging and tracing, essential for identifying and fixing issues in your optimization models.
Understanding relational semantics will help you grasp how different parts of your model interact, ensuring you don’t end up with too many or too few solutions.
Improving your models is a key focus, and you’ll learn to do this through practical workshops, like the poetry challenge and the elephant weighing exercise.
These aren’t just fun—they’re designed to solidify your learning through real-world applications.
The course also covers scheduling in-depth, from the basics to more complex sequence-dependent scheduling.
This knowledge is invaluable for organizing tasks in a range of industries.
Packing problems are part of the curriculum too.
You’ll explore various strategies, including square and rectilinear packing, which are crucial for fields like logistics and manufacturing.
Symmetries and dominance in models can be tricky, but this course will teach you how to navigate these issues, enhancing the power and efficiency of your models.
Throughout the course, you’ll use MiniZinc, a leading tool for building decision support systems, under the guidance of Professor Mark Wallace, an expert in the field.
This hands-on experience with MiniZinc will give you a practical edge.
By the end of the course, you’ll have tackled historical and modern optimization challenges, rounding off your experience with a reflective survey.
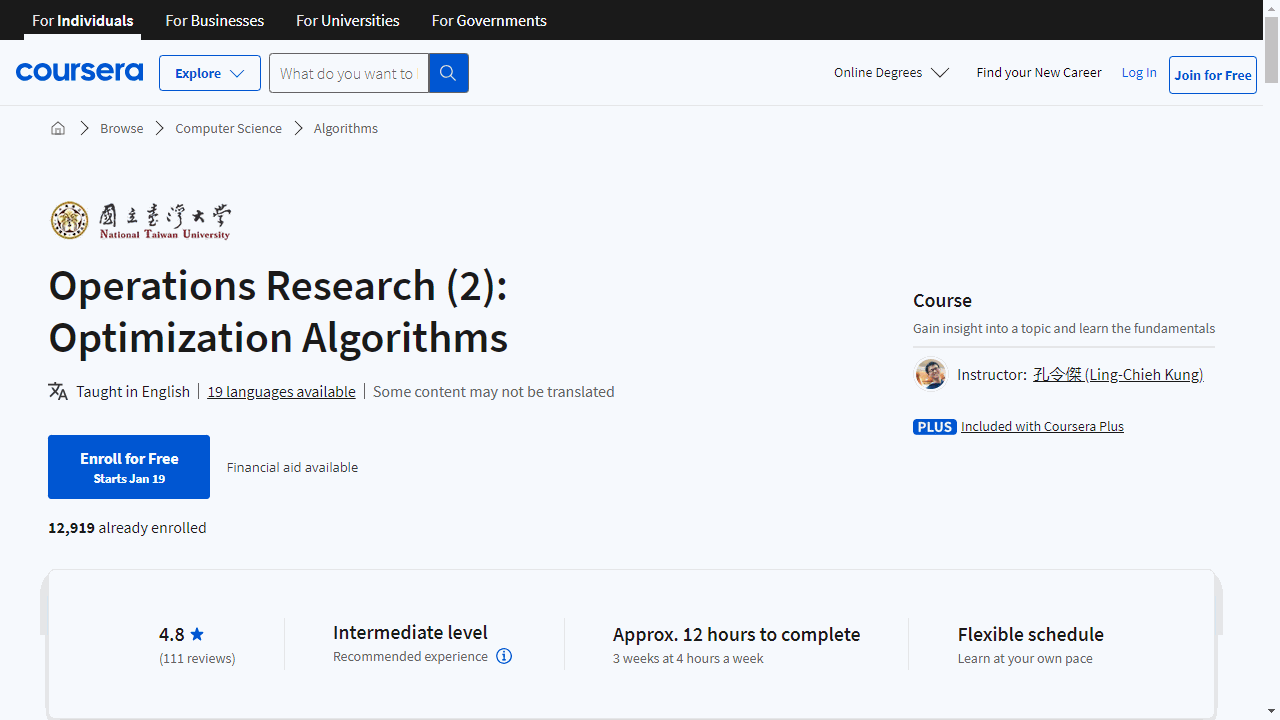
Operations Research (2): Optimization Algorithms
Provider: National Taiwan University
This course equips you with a deep understanding of optimization algorithms, crucial for solving complex problems in various industries.
You’ll start with the essentials, learning about linear systems and how to solve them using techniques like Gaussian elimination.
This foundational knowledge is critical as it underpins the more advanced topics you’ll encounter later.
As you progress, the course delves into linear programming (LPs), where you’ll master the simplex method, a cornerstone algorithm for optimization.
You’ll learn to identify extreme points, understand basic solutions, and apply the simplex method through practical examples, ensuring you grasp the concepts thoroughly.
Branch and bound methods are also covered, teaching you how to break down intricate problems into simpler ones, a skill that’s invaluable when facing real-world challenges.
The course also tackles the knapsack problem, illustrating the principles of optimization in a tangible way.
A unique feature of this course is its hands-on approach to technology.
You’ll learn to use Python and Gurobi, tools that are essential for implementing LPs in professional settings.
This practical experience bridges the gap between theory and application, giving you a competitive edge.
The course doesn’t stop at linear problems.
You’ll explore gradient descent and Newton’s method for tackling nonlinear problems, learning how to navigate the complexities of these equations and find optimal solutions efficiently.
Modeling is the final piece of the puzzle, where you’ll learn to create models that accurately represent real-life scenarios.
You’ll even develop your own heuristic algorithm, enhancing your problem-solving toolkit.
Throughout the course, performance evaluation is emphasized, ensuring you can assess the effectiveness of your solutions.
The curriculum is thoughtfully structured, building your knowledge step by step.
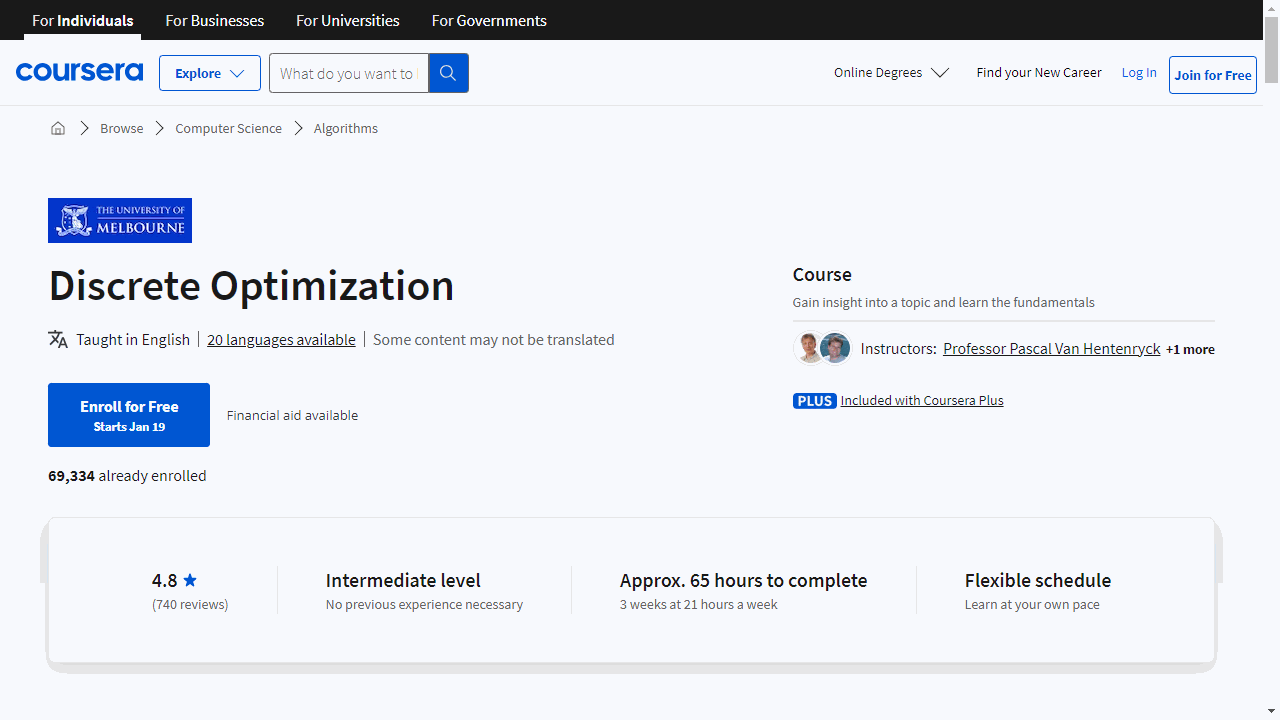
Discrete Optimization
This course is a practical, hands-on journey through the world of optimization, designed to equip you with the skills to solve complex real-world problems.
You’ll start with the knapsack problem, learning to pick the best combination of items for maximum value.
This isn’t just theory; you’ll apply techniques like dynamic programming and branch and bound to find solutions.
Next, you’ll master constraint programming (CP), a powerful tool that helps you set rules and let the computer do the heavy lifting.
You’ll solve puzzles like Sudoku and tackle scheduling issues, such as planning a wedding seating chart without the stress.
Local search (LS) strategies come into play as you learn to make incremental changes to improve solutions.
This method is key for optimizing routes for delivery trucks or creating efficient sports tournament schedules.
The course also covers linear programming (LP), a critical decision-making tool for complex scenarios.
You’ll navigate through multiple options to find the most efficient path, much like choosing the best route on a map.
For more intricate problems, you’ll delve into mixed-integer programming (MIP), which handles decisions that are binary, like on/off switches.
This technique is essential for real-life applications, such as warehouse location planning and truck routing.
As you progress, you’ll tackle assignments that mirror real-life challenges, from facility location to vehicle routing.
You’ll learn to avoid solution dead-ends and employ algorithms like simulated annealing, inspired by metallurgy, to refine your results.
By the end of this course, you’ll not only have a toolkit of optimization methods but also practical experience in applying them.
Whether it’s using the simplex algorithm, breaking symmetries, or understanding the nuances of heuristics, you’ll be ready to tackle any optimization challenge.
If you’re passionate about finding the best solutions and eager to apply math and computing to real-world issues, this Discrete Optimization course is tailored for you.
It’s not just about learning; it’s about applying knowledge to navigate and conquer the optimization landscape.
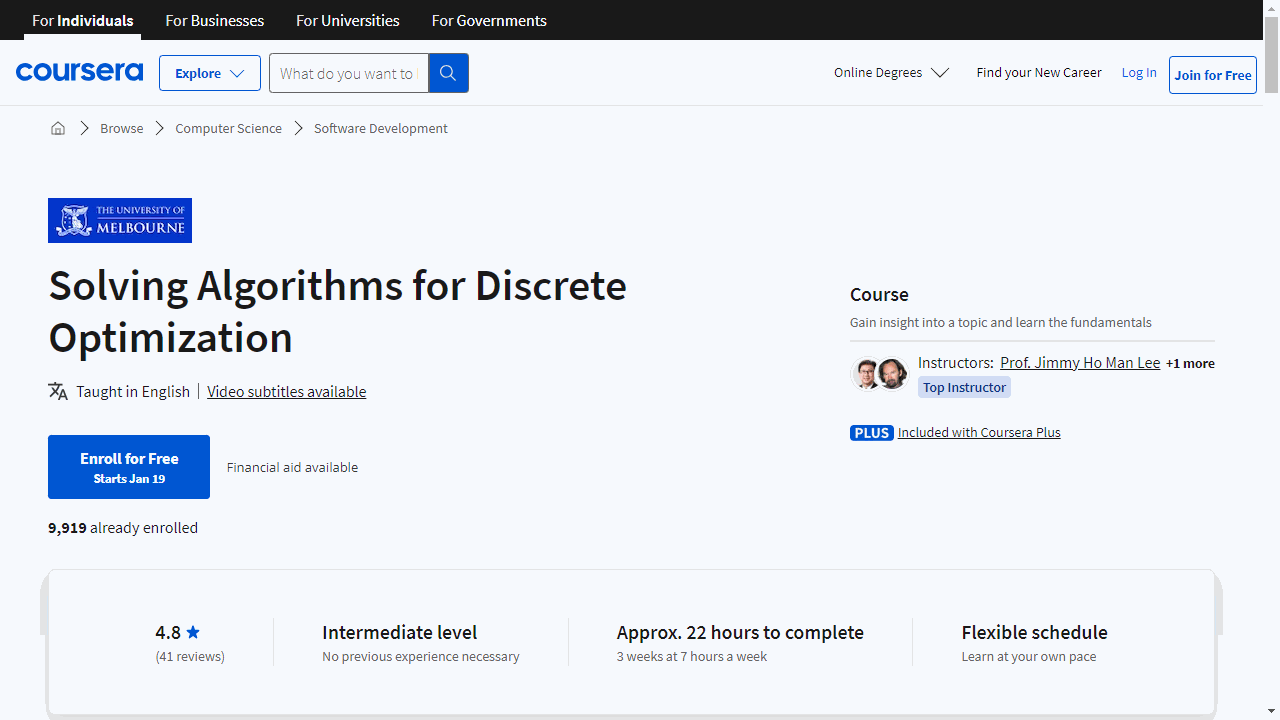
Solving Algorithms for Discrete Optimization
You’ll start by mastering Constraint Programming Solvers, learning how to set up problems with specific rules and find fitting solutions.
It’s like crafting a custom puzzle and solving it piece by piece.
You’ll understand the importance of Domains and Propagators in defining these problems.
As you progress, you’ll delve into Bounds Propagation and the Propagation Engine, honing your ability to eliminate impossible solutions quickly.
This is crucial for focusing your efforts on viable options.
The course also covers various search strategies, teaching you how to sift through potential solutions to find the optimal one.
With Optimization in CP, you’ll not just find any solution, but the best one for your specific problem.
Advanced topics such as Restart and Advanced Search strategies will be demystified, giving you insight into the intricacies of constraints like Alldifferent and Cumulative.
You’ll also explore Linear Programming and Mixed Integer Programming, which are essential for problems involving both whole numbers and fractions.
Cutting Planes techniques and the application of MiniZinc to MIP will further enhance your problem-solving toolkit.
You’ll be able to slice through complex issues with precision and apply modeling tools effectively.
Local Search strategies will introduce you to methods for navigating vast solution spaces.
Techniques like Escaping Local Minima, Simulated Annealing, and Large Neighbourhood Search will empower you to avoid settling for subpar solutions and instead aim for the best possible outcome.
Practical workshops, including “Birthday Parade” and “Banquet Preparation,” provide hands-on experience, allowing you to apply your newfound knowledge to real-world scenarios.
The course culminates with the “Refugee Assignment” workshop, where you’ll employ all your skills to solve a challenging problem.
Basic Modeling for Discrete Optimization
This course gives you a practical understanding of how to model and solve optimization problems using MiniZinc, a leading tool in the field.
Starting with the basics, you’ll quickly learn to construct your first models, which are essential for simplifying complex decisions.
The course is structured to build your skills progressively, introducing you to arrays, comprehensions, and global constraints—key elements in creating effective optimization models.
What sets this course apart is its hands-on approach.
Through workshops, you’ll apply your new knowledge to solve problems like temperature regulation and strategic planning.
This real-world application ensures that the concepts you learn are not only understood but also retained.
As you delve deeper, the course covers set representations and functions, teaching you about cardinality and how to manage sets with specific limitations.
You’ll also master permutations, a concept vital for arranging data in optimization problems.
Guidance comes from experts like Professor Mark Wallace, who brings a wealth of knowledge in decision support systems.
The course is rich with reference materials, including solutions to workshops, allowing you to learn from both successes and mistakes.
Optimization for Decision Making
Provider: University of Minnesota
If you’re eager to enhance your decision-making with robust optimization skills, this course stands out with its practical approach, expert instruction, and real-world applicability.
This course is a key part of the University of Minnesota’s “Analytics for Decision Making” specialization and is crafted to equip you with the skills to apply optimization techniques effectively in various decision-making scenarios.
Under the guidance of Soumya Sen, you’ll start with the essentials of Linear Programming.
This means you’ll learn to navigate decision-making with specific constraints, a skill that’s invaluable in both business and everyday problem-solving.
You’ll get hands-on experience with practical examples, such as optimizing operations for a brewery or a furniture company.
These aren’t just theoretical exercises; they’re designed to mirror real-life challenges and show you the direct application of optimization.
The course progresses to more complex problems, teaching you how to handle situations with multiple solutions or seemingly incompatible rules.
You’ll also become adept at understanding the implications of changes to model parameters, a critical aspect of optimization.
A highlight of the course is the module on using Excel for optimization.
Far from mundane, this section will show you how to harness the power of Excel’s Solver tool to tackle and solve optimization problems efficiently.
You’ll follow clear, step-by-step instructions to build and solve your own models, culminating in a “Make vs. Buy” decision exercise for a gaming company.
Upon completion, you’ll not only receive congratulations but also information on further educational opportunities in Business Analytics, should you wish to deepen your expertise.
Optimization Methods in Asset Management
Provider: Columbia University
This course equips you with the expertise to craft optimal portfolios and navigate the complexities of investment strategies.
Starting with the basics, you’ll learn to construct optimal portfolios and explore the efficient frontier using Excel—a vital tool for practical asset management.
The course introduces you to foundational concepts such as the Two Fund and One Fund Theorems, which guide the combination of risky and risk-free assets for maximum efficiency.
You’ll also delve into advanced topics like the Sharpe Optimal Portfolio and the Capital Asset Pricing Model (CAPM), which are essential for understanding risk-return relationships.
Hands-on Excel exercises will help you master plotting the Security Market Line, a critical skill for evaluating investment risk.
When markets are unpredictable, the course has you covered.
You’ll learn to use Value at Risk (VaR) and Conditional Value at Risk (CVaR) to assess potential losses in different market scenarios.
This prepares you to make informed decisions even during volatile times.
A unique aspect of this course is its focus on identifying and avoiding biases that can distort investment analysis.
You’ll learn to recognize and sidestep common pitfalls like survivorship bias and data snooping, ensuring your investment strategy is based on sound data.
Beyond theory, the course dives into the practicalities of liquidity and trading costs.
You’ll gain insights into optimal trade execution and understand how to minimize costs, enhancing your trading strategies with practical Excel exercises.
Throughout the course, quizzes and assignments reinforce your learning, ensuring you can apply these concepts effectively.
Columbia University maintains a strict academic honesty policy, fostering a fair and rigorous learning environment.
Supply Chain Optimization
Provider: University of California, Irvine
If you’re eager to enhance your supply chain skills with a practical, example-rich course, UC Irvine’s offering might just be the key to unlocking your potential.
It’s designed to give you hands-on experience with the tools and techniques that make supply chains more efficient and cost-effective.
You’ll start with the basics of optimization, understanding its role in streamlining operations, much like finding the quickest route to your destination.
From there, you’ll delve into capacity optimization, learning to balance workload and resources to avoid bottlenecks – think of it as packing your suitcase just right.
Resource optimization is up next, where you’ll tackle minimizing costs while maximizing output.
It’s like planning a party with the best possible use of your budget.
This part of the course will teach you to make the most of what you have.
The highlight is the Monte Carlo Simulation, a powerful tool that predicts outcomes and improves decision-making in supply chains.
You’ll get to grips with this technique, using it to analyze performance and explore various scenarios, much like strategizing in a game to find the winning approach.
As you progress, you’ll reflect on each concept, connecting the dots to see the bigger picture of supply chain management.
By the end of the course, you’ll be equipped with a set of strategies to optimize any supply chain, ready to make impactful, cost-saving decisions.